
Unraveling the Secrets of Triangular Prism Volume: A Comprehensive Guide
Have you ever wondered how to calculate the volume of an object with unusual shapes like a triangular prism? It’s a common question in geometry that often sparks curiosity and perplexity. Let’s embark on a journey to demystify the concept of volume in a triangular prism and explore practical applications.
Understanding Triangular Prisms: A Geometric Excursion
A triangular prism is a three-dimensional geometric shape with two parallel triangular faces called bases, connected by three rectangular faces called lateral surfaces. The height of the prism is the perpendicular distance between the two bases. The volume of a triangular prism is the amount of space it occupies in three-dimensional space.
Calculating Triangular Prism Volume:
Calculating the volume of a triangular prism is relatively straightforward. The formula for finding the volume is:
V = (1/2) * B * hWhere:
- V is the volume of the prism in cubic units
- B is the area of the base in square units
- h is the height of the prism in units
Breaking Down the Formula:
- Area of the Base (B): The base of a triangular prism is a triangle. To calculate the area of a triangle, you need to use the formula:
Area of triangle = (1/2) * b * hWhere:
- b is the base of the triangle in units
- h is the height of the triangle in units
- Height of the Prism (h): The height of a triangular prism is the distance between the two bases. Measure in units.
Application of Volume Calculation:
Understanding the volume of a triangular prism has practical applications in various fields. For instance, in architecture, it helps determine the volume of a building’s interior space. In engineering, it allows engineers to calculate the volume of fuel tanks or reservoirs. In packaging and logistics, it enables manufacturers to determine the size of boxes or containers required to accommodate specific products.
Tips for Accurate Volume Determination:
-
Precise Measurements: Ensure accurate measurements of the base and height to avoid inaccuracies in the volume calculation.
-
Careful Unit Conversion: If the measurements are in different units, convert them to a consistent unit system (e.g., centimeters or inches) before performing the calculation.
-
Double-Checking: Once the calculation is complete, double-check the values and formula to minimize errors.
FAQ on Triangular Prism Volume:
Q: What is the SI unit for volume?
A: Cubic meters (m³)
Q: Can the formula be used to calculate the volume of any triangular prism?
A: Yes, as long as the base is a triangle.
Q: How do I find the volume of a triangular prism with a parallelogram base?
A: Convert the parallelogram base into a triangle by drawing a diagonal and then use the formula for triangular prism volume.
Conclusion
Mastering the calculation of triangular prism volume provides a fundamental understanding of geometry and its applications in practical scenarios. Remember, the volume is a measure of the three-dimensional space occupied by the prism and is essential for various tasks in fields like architecture, engineering, and packaging.
Are you interested in exploring other geometrical concepts and their applications? Share your thoughts and questions below, and let’s continue our mathematical journey together.

Source Image: www.elevise.co.uk

Source Image: www.elevise.co.uk
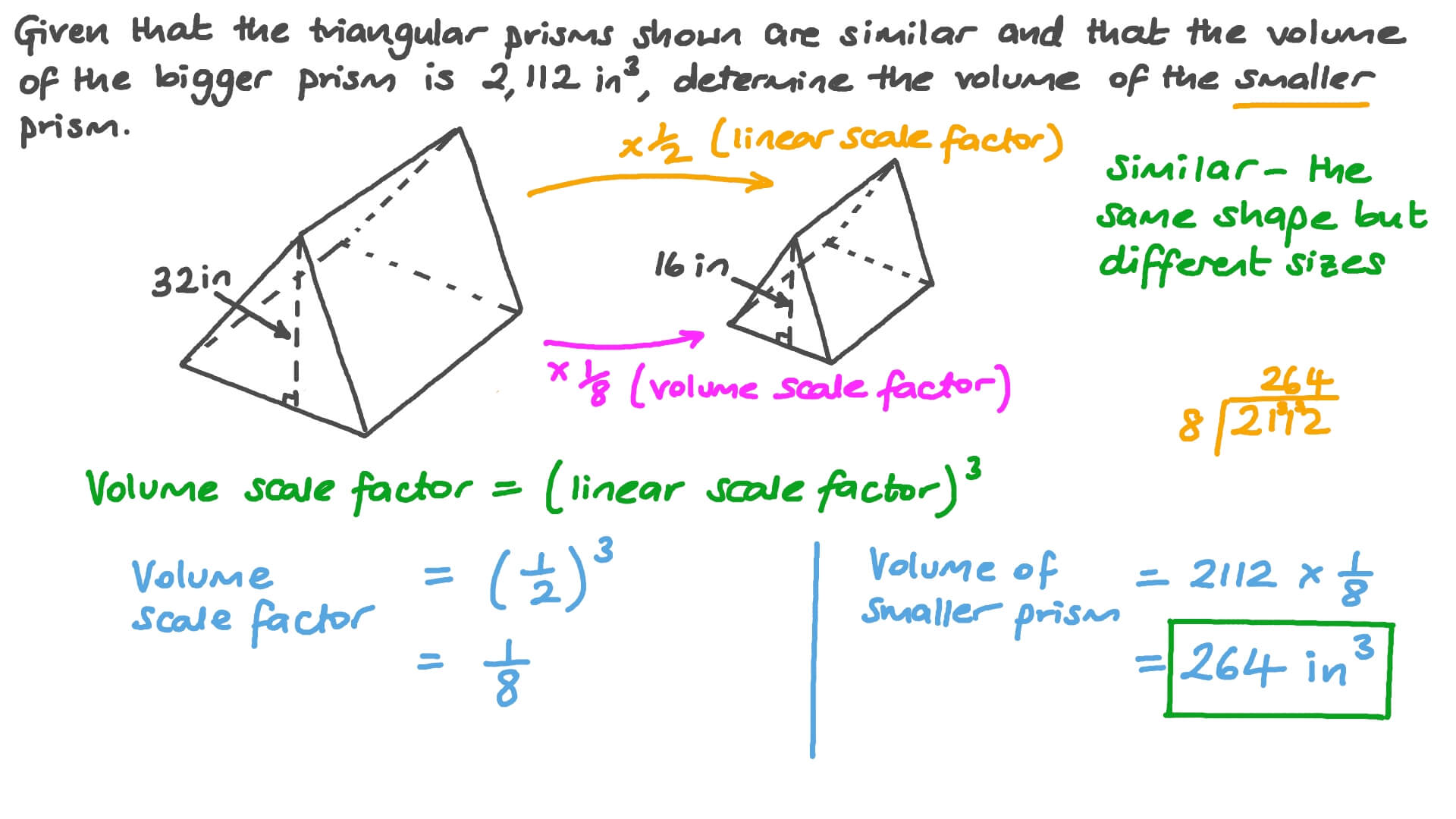
Source Image: www.elevise.co.uk
Thank you for your animated engagement with this material. The Volume Of The Triangular Prism Is 54 Cubic Units, is a fantastic resource for broadening your perspective.