Select All Of The Following Graphs Which Are One-To-One Functions. – is the article you’re looking for. Hopefully, you’ll find information related to Select All Of The Following Graphs Which Are One-To-One Functions., all of which we’ve summarized from various reliable sources.

One-to-One Functions: A Comprehensive Guide
An Introduction to Functions
Functions, a fundamental concept in mathematics, represent relationships between sets of values. A function, denoted as f(x), assigns a unique output value for every input value within its domain. Functions play a crucial role in various fields, including calculus, algebra, and science, providing a means to model and analyze real-world phenomena.
One-to-One Functions
Among the diverse types of functions, one-to-one functions, also known as invertible functions, possess a unique characteristic. A function f(x) is considered one-to-one if for every distinct input value x1 and x2 within its domain, the corresponding output values f(x1) and f(x2) are also distinct.
The Horizontal Line Test
One convenient method to determine whether a function is one-to-one is through the horizontal line test. If any horizontal line intersects the graph of the function more than once, the function fails the test and is not one-to-one. Conversely, if every horizontal line intersects the graph at most once, the function passes the test and is considered one-to-one.
Examples of One-to-One Functions
- Linear Function: f(x) = mx + b, where m ≠ 0
- Quadratic Function: f(x) = x2, when restricted to a specific domain
- Exponential Function: f(x) = ex
- Logarithmic Function: f(x) = logb(x), where b > 0 and b ≠ 1
Examples of Non-One-to-One Functions
- Constant Function: f(x) = c, where c is a constant
- Quadratic Function: f(x) = -x2
- Absolute Value Function: f(x) = |x|
- Greatest Integer Function: f(x) = [x]
Applications of One-to-One Functions
One-to-one functions are invaluable in various mathematical applications, such as:
- Cryptography: Creating encryption algorithms that maintain data privacy
- Data Analysis: Identifying unique values in datasets
- Computer Science: Designing hashing functions for efficient data storage and retrieval
Tips and Expert Advice
When dealing with one-to-one functions, several practical tips and expert advice can enhance your understanding:
- Visualize the Graph: Sketching the graph of the function can help you determine if it passes the horizontal line test.
- Check for Inverses: A function is one-to-one if and only if it has an inverse function.
FAQs on One-to-One Functions
Q: What is the difference between a one-to-one function and a many-to-one function?
A: In a one-to-one function, each input value corresponds to a unique output value. In a many-to-one function, multiple input values can map to the same output value.
Q: How can I determine the inverse of a one-to-one function?
A: To find the inverse of a one-to-one function f(x), simply swap the roles of x and y in the equation, f(x) = y, to obtain y = f-1(x).
Q: Are all linear functions one-to-one?
A: Yes, all linear functions with a non-zero slope are one-to-one.
Conclusion
One-to-one functions serve as a vital tool in mathematics and its applications. Understanding their properties and characteristics is crucial for mathematicians, Scientists, and students alike. By utilizing the horizontal line test, recognizing common examples, and exploring their applications, individuals can gain a comprehensive understanding of these functions.
Are you interested in delving deeper into the world of one-to-one functions? Explore additional resources, engage with experts in online forums, and challenge your knowledge through practice problems.
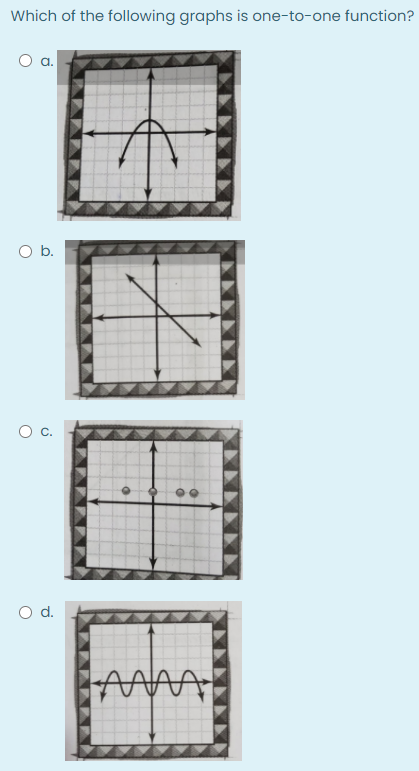
Image: www.bartleby.com
You have read Select All Of The Following Graphs Which Are One-To-One Functions. on our site. Thank you for your visit, and we hope this article is beneficial for you.